How to write the fastest cosine-similarity function?
Computing cosine similarity in the fastest possible way.
Writing fast cosine similarity function is a million-dollar problem. No seriously. Companies like Pinecone, and Milvus, have raised millions of dollars to build a vector database.
In neural network models, words, images, and documents are represented as vectors. They capture information that can be used to quantify the relationship between two entities. One operation used to measure ‘similarity’ between two entities is the cosine between their vectors. For example, how similar two images are can be quantified using the cosine similarity between their vectors.
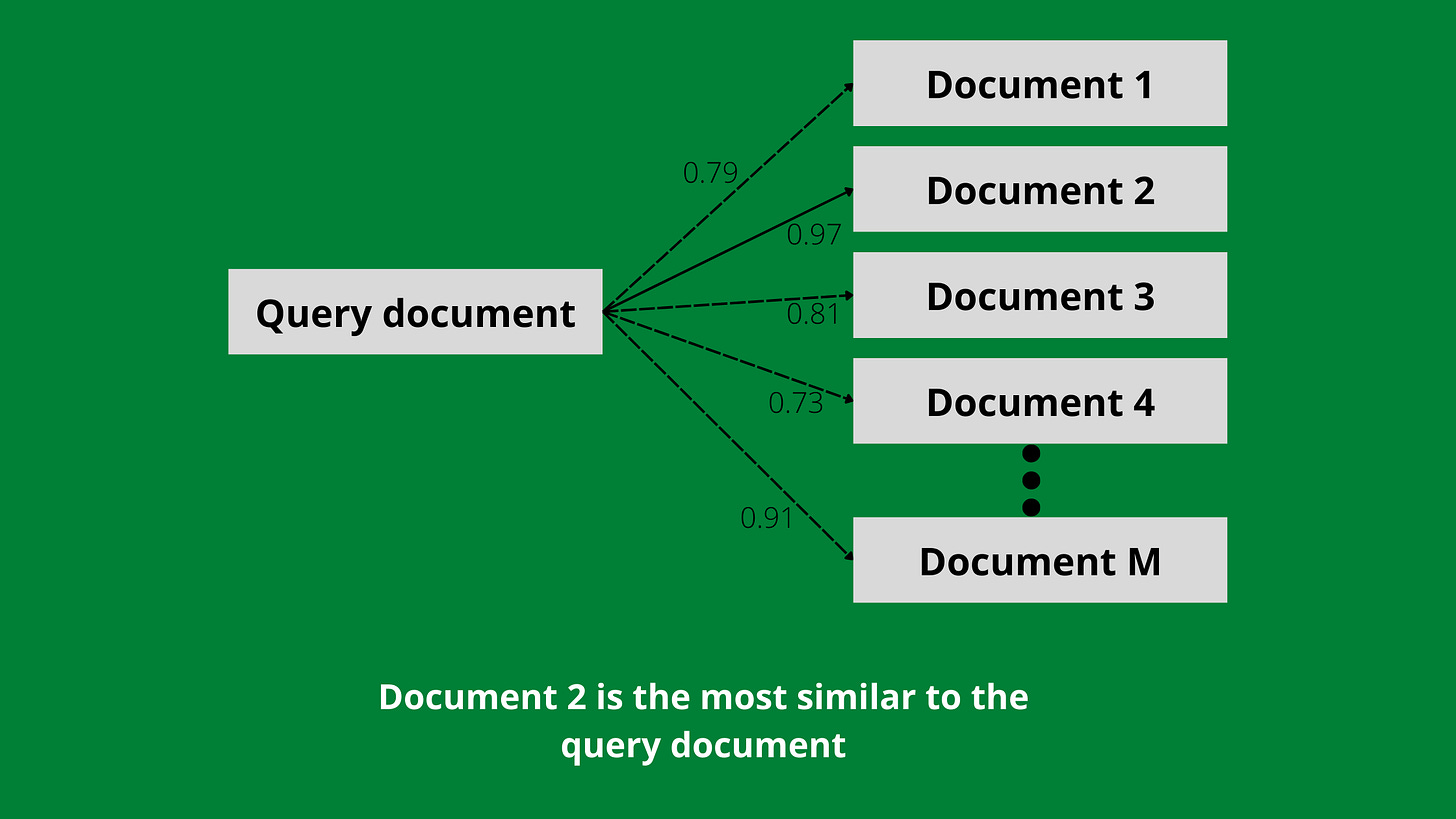
Consider a database of M documents, each having its vector. The task is to find the most (or k most) similar document for a query document (having its vector) from this database, also referred to as nearest neighbour search.
Easy. Compute the cosine similarity of this query vector with the M vectors, and return the document corresponding to the highest similarity.
For vectors with d dimensions, each cosine similarity computation has O(d) time complexity, and for M such operations, O(M*d). As M increases, the overall compute time increases, which is not good. Hence, we wish to make this process as quick and scalable as possible. In industry, there are two ideas to do a nearest neighbour search - Exact and Approximate.
An exact (or brute-force) search finds the similarity from all vectors in the database for a query, which is expensive, but truly gives you the nearest neighbour. On the contrary, an approximate search sacrifices the exactness for a faster search. The result will not be THE nearest neighbour, but somewhere pretty close. In this post, I primarily focus on making the exact search faster.
The rest of the article will benchmark different Python implementations of the nearest neighbour search. Towards the end, I discuss the pros and cons and choose a winner!
Setup
The document corpus is represented by a random NumPy matrix (float64) of 1 million rows (=M). I say ‘document corpus’, but it might as well be images or audio. As mentioned previously, all modalities are represented by vectors. Besides, we are concerned with cosine similarity computation, which is an independent problem.
I formed a set of 1000 random queries with the same number of features as the document matrix. Next, I compute cosine similarity in a batch fashion. This means concatenating all the queries and sending them to the function instead of one at a time.
Based on popular Python frameworks and libraries, our candidate implementations include
Pure NumPy
SciPy
Numba (Numba, in their own words, is an open source JIT compiler that translates a subset of Python and NumPy code into fast machine code.). Write a function in Python or NumPy and then compile it using Numba’s JIT compiler.
I investigate two different implementations using Numba.Pythonic - The cosine similarity function, written in pure Python using nested for loops, is compiled using Numba.
NumPy based - The cosine similarity function is written using NumPy APIs and then compiled with Numba.
FAISS (FAISS, in their own words, is a library for efficient similarity search and clustering of dense vectors. It contains algorithms that search in sets of vectors of any size, up to ones that possibly do not fit in RAM.)
In each implementation, I varied the vector dimension d (set to 32, 64, 128, 256) to observe the effect of d on the speed.
Implementation
I ran all the implementations on Google colab pro (with high RAM runtime). The code for this exercise is available here.
Pure NumPy
Scipy
Pythonic Numba
NumPy based Numba
FAISS
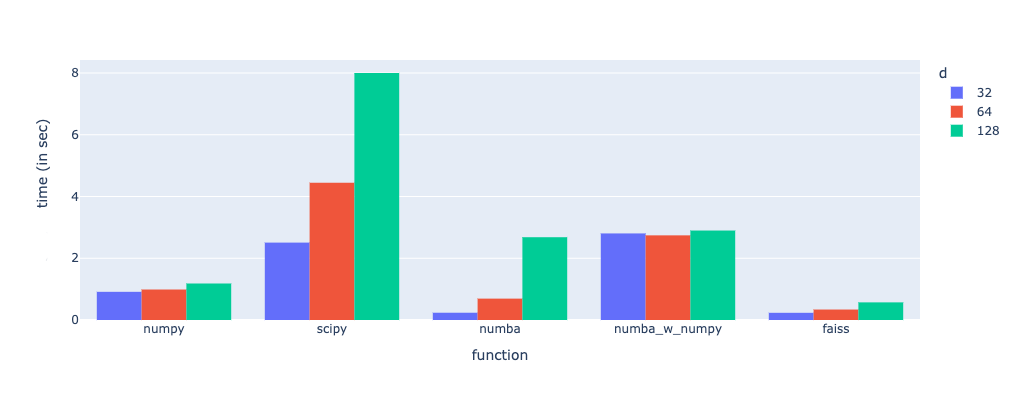
Results
Note that the operations were optimized by normalizing the document matrix beforehand, requiring only the query matrix normalized at run time.
In the figure above, the x-axis labels -
numpy → Pure Numpy implementation
scipy → Scipy based implementation
numba → Pythonic Numba implementation
numba_w_numpy → NumPy based Numba implementation
faiss → FAISS based implementation
Observations
SciPy is the slowest and gets worse with increasing d.
FAISS is the fastest of all, and it scales well with d.
Pythonic Numba is a great candidate but gets worse with increasing d
NumPy-based Numba performs worse than Pythonic Numba.
Some notes on the results
In this section, I explain our findings and the function implementation wherever necessary.
Why is SciPy so slow?
One reason is that SciPy normalizes both the arrays (query and document) each time the cdist function is called. However, the document array is already normalized, and thus SciPy does some repeat work.
This part of SciPy’s implementation is found here.

Why Numba compiled Numpy is slower than Numba compiled Python implementation?
I Googled this question and found a very high-level answer. Quoting the solution from here
For larger matrices, a BLAS call from compiled code is faster, for smaller matrices custom Numba or Cython Kernels are usually faster.
This explains why the time taken for d=128 by both the Numba implementation is almost the same.
Conclusion
FAISS is one of the fastest, highly scalable, easy-to-implement open-source nearest neighbour search frameworks. I wish to do this exercise for an approximate search in one of the following articles. If you found this article helpful, subscribe to my newsletter!